Kaleidoscopic Cells

Many triply periodic minimal surfaces can best be understood and constructed in terms of fundamental regions bounded by mirror symmetry planes. According to H. S. M. Coxeter (Regular Polytopes, p. 84) there are exactly seven types of such regions of finite size. These are shown here, with commentary relevant to triply periodic minimal surfaces.

Many triply periodic minimal surfaces have embedded straight lines, which of necessity must be C2 symmetry axes (180 degree rotational symmetry). Possible C2 axes are shown in color below.

There are two classes of kaleidoscopic cells: the prisms and the tetrahedra. A prism in the general sense is a plane polygon extended at right angles in the third dimension. A tetrahedron is a polyhedron with four flat faces.

Prisms

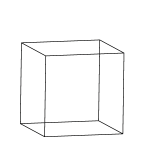
rectangular_parallelpiped

Rectangular Parallelepiped

A rectangular box, shown in its maximally symmetric form of a cube.		 rectangular parallelpiped
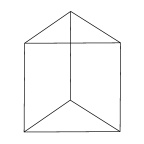
equilateral prism

Equilateral Prism

A prism based on an equilateral triangle.		 equilateral prism
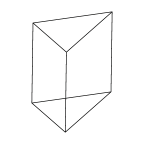
isoceles prism

Isosceles Prism

A prism based on a 45-45-90 degree triangle.		 isoceles prism
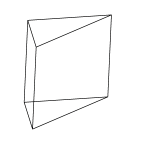
30-60-90 prism

30-60-90 Prism

A prism based on a 30-60-90 degree triangle.		 30-60-90 prism

Tetrahedra

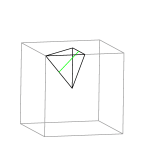
quadrirectangular tetrahedron

Quadrirectangular Tetrahedron

This tetrahedron is shown as 1/48 of a cube; it is the fundamental
region for the full symmetry group of the cube. There is one possible
C2 axis, shown in green. The name quadrirectangular refers
to the fact that each of the four faces has a right angle.		 quadrirectangular tetrahedron
trirectangular tetrahedron

Trirectangular Tetrahedron

This tetrahedron is shown as 1/24 of a cube. There are no possible C2 axes.		 trirectangular tetrahedron
disphenoid

Tetragonal Disphenoid

This tetrahedron can be viewed as two trirectangular tetrahedra
stacked up. There are three possible C2 axes, shown in green and red. 		disphenoid
Back to periodic minimal surfaces.
Back to Ken Brakke's home page.