

Ken Brakke
Professor Emeritus
Department of Mathematics
and Computer Science
Susquehanna University
Phone: 570-495-0452 (mobile)
Email:
brakke@susqu.edu
Snail mail: 2603 Pacific Highlands Ave, Ferndale, WA 98248


Version 2.70, August 25, 2013
My Surface Evolver is an interactive program for the modelling of liquid
surfaces shaped by various forces and constraints. The program is
available free of charge.
Jean Berthier and I have collaborated on a book about the behavior of
liquids in microfluidic circumstances. Over a hundred Evolver models,
available for download from the book's website (if you buy the book).
Jean Berthier and I have done another book, about liquids flowing
in channels that are not completely enclosed.
Includes lots Evolver models,
available for download from the book's website (if you buy the book).
The result of my amateur attempt to translate Joseph Plateau's famous
1873 book on soap films and surface tension.
A gallery
of random fractal images generated with iterated function
systems (IFS), along with my own applet to generate more. Infinite
complexity and amazing variety from simple rules!
A program for visualizing multiple universes connected by gateways formed by
cosmic strings. The image shows five universes (with different color skies)
connected by a string in the shape of a trefoil knot. Polycut reveals how soap
films are least-area
boundaries between universes.
What is the least area way to partition space into unit volumes?
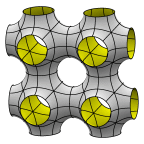 Surfaces of zero mean curvature that repeat
periodically in three dimensions.
Surfaces of zero mean curvature that repeat
periodically in three dimensions.

Which soap films on wire frames form perfect cones straight to the center?
There are surprisingly few.

Knotted wires make for some very interesting soapfilms!
The Borromean Rings are three rings linked so that any pair of rings are
not linked, but all three are (i.e. cannot be pulled apart). The Rings
support many soap films.
For 3D mouse-spinnable images using the upcoming WebGL 3D
technology, go
here. (Only works on FireFox 4 Beta or later,
suitably configured. Before loading, browse "about:config" and
set "webgl.enabled_for_all_sites" to "true"; this setting will be
permanently remembered.)
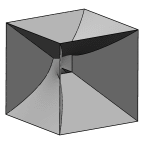
What is the least area surface that can block any ray of light from
passing through the interior of a cube?

Even if the galaxy potentially has millions of space-faring civilizations,
the first such civilization probably gets about a
100 million year head start on the second. We look to be the first,
so the galaxy is ours to colonize without opposition!
A Surface Evolver simulation
of 2D grain growth, starting with 100 grains. The starting configuration
is the Voronoi diagram of 100 random points. Periodic boundary conditions.
1.6MB mpeg. Also 1000 grain movie
(8 MB mpeg) and 10000 grain movie
(10 MB mpeg).
These are mainly for the benefit of my Geometry class. There are
step-by-step constructions for 29 basic constructions, plus some
more challenging ones.
 My papers.
My papers.













 My papers.
My papers.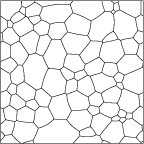 Grain growth movie.
Grain growth movie.  Ruler and compass constructions.
Ruler and compass constructions.