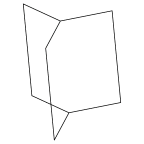
Frame
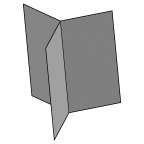
Minimal cone
(VRML)
In the examples below, clicking on the small image will get a full-screen version the image. You can get a 3D version by clicking on the VRML tag below a picture, if you have a VRML2 viewer.
These images were generated with my Surface Evolver program. The Evolver datafile names are in parentheses. The datafiles contain commands to evolve the surfaces shown here. The VRML files were generated by the Evolver using my vrml2.cmd script.
 Frame |
 Minimal cone (VRML) |
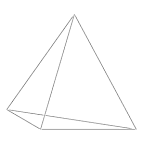 Frame |
 Minimal cone (VRML) |
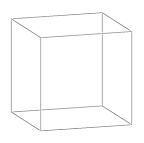 Frame |
 Cone (VRML) |
 Better film (VRML) |
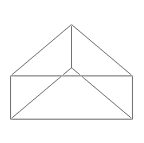 Frame |
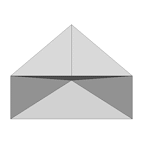 Cone (VRML) |
 Better film (VRML) |
 Frame |
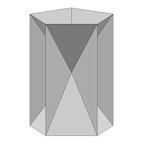 Cone (VRML) |
 Better film (VRML) |
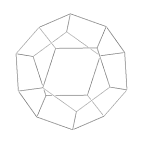 Frame |
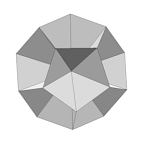 Cone (VRML) |
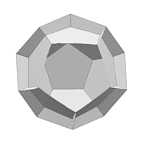 Better film (VRML) |
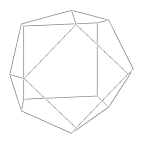 Frame |
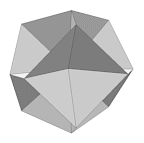 Cone (VRML) |
 Better film (VRML) |
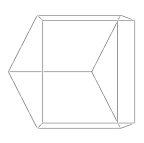 Frame |
 Cone (VRML) |
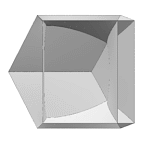 Better film (VRML) |
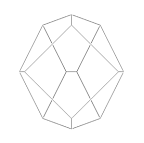 Frame |
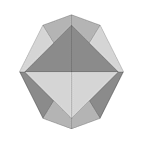 Cone (VRML) |
 Better film (VRML) |