ZH.
On each plane there is a circular pad
that the solder perfectly wets, and the solder is perfectly nonwetting
off the pads. This would be just a catenoid problem with fixed volume,
except that the pads are offset, and it is desired to find out what
aligning force the solder exerts. The surface is defined the same
way as in the catenoid example, except the lower boundary ring has
a shift variable SHIFT in it to provide an offset in the
y direction.
This makes the shift adjustable at run time.
Since the top and bottom
facets of the body are not included, the constant volume they account
for is provided by content integrals around the upper
boundary, and the gravitational energy is provided by an energy
integral.
One could use the volconst attribute of the body instead for the volume,
but then one would have to reset that every time ZH changed.
The interesting part of this example is the calculation of the forces. One could incrementally shift the pad, minimize the energy at each shift, and numerically differentiate the energy to get the force. Or one could set up integrals to calculate the force directly. But the simplest method is to use the Principle of Virtual Work by shifting the pad, recalculating the energy without re-evolving, and correcting for the volume change. Re-evolution is not necessary because when a surface is at an equilibrium, then by definition any perturbation that respects constraints does not change the energy to first order. To adjust for changes in constraints such as volume, the Lagrange multipliers (pressure for the volume constraint) tell how much the energy changes for given change in the constraints:
DE = L*DCwhere
DE is the energy change,
L is the row vector of Lagrange multipliers and DC is the column
vector of constraint value changes. Therefore, the adjusted energy
after a change in a parameter is
E_adj = E_raw - L*DCwhere
E_raw is the actual energy and DC is the vector of differences of
constraint values from target values. The commands do_yforce and
do_zforce in the datafile do central difference calculations of the
forces on the top pad, and put the surface back to where it was
originally. Note that the perturbations are made smoothly, i.e. the
shear varies linearly from bottom to top. This is not absolutely
necessary, but it gives a smoother perturbation and hence
a bit more accuracy.
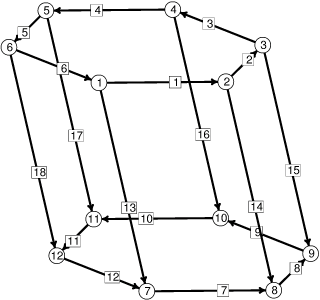
 |
The initial column skeleton, with vertices and edges numbered. |
// column.fe
// Example of calculating forces exerted by a
// column of liquid solder in shape of skewed catenoid.
// All units cgs
parameter RAD = 0.05 // ring radius
parameter ZH = 0.08 // total height
parameter SHIFT = 0.025 // shift
#define SG 8 // specific gravity of solder
#define TENS 460 // surface tension of solder
#define GR 980 // acceleration of gravity
gravity_constant GR
BOUNDARY 1 PARAMETERS 1
X1: RAD*cos(P1)
X2: RAD*sin(P1) + SHIFT
X3: ZH
CONTENT // used to compensate for missing top facets
c1: 0
c2: -ZH*x
c3: 0
ENERGY // used to compensate for gravitational energy under top facets
e1: 0
e2: GR*ZH^2/2*x
e3: 0
BOUNDARY 2 PARAMETERS 1
X1: RAD*cos(P1)
X2: RAD*sin(P1)
X3: 0
vertices // given in terms of boundary parameter
1 0.00 boundary 1 fixed
2 pi/3 boundary 1 fixed
3 2*pi/3 boundary 1 fixed
4 pi boundary 1 fixed
5 4*pi/3 boundary 1 fixed
6 5*pi/3 boundary 1 fixed
7 0.00 boundary 2 fixed
8 pi/3 boundary 2 fixed
9 2*pi/3 boundary 2 fixed
10 pi boundary 2 fixed
11 4*pi/3 boundary 2 fixed
12 5*pi/3 boundary 2 fixed
edges
1 1 2 boundary 1 fixed
2 2 3 boundary 1 fixed
3 3 4 boundary 1 fixed
4 4 5 boundary 1 fixed
5 5 6 boundary 1 fixed
6 6 1 boundary 1 fixed
7 7 8 boundary 2 fixed
8 8 9 boundary 2 fixed
9 9 10 boundary 2 fixed
10 10 11 boundary 2 fixed
11 11 12 boundary 2 fixed
12 12 7 boundary 2 fixed
13 1 7
14 2 8
15 3 9
16 4 10
17 5 11
18 6 12
faces
1 1 14 -7 -13 density TENS
2 2 15 -8 -14 density TENS
3 3 16 -9 -15 density TENS
4 4 17 -10 -16 density TENS
5 5 18 -11 -17 density TENS
6 6 13 -12 -18 density TENS
bodies
1 -1 -2 -3 -4 -5 -6 volume 0.00045 density SG
read
// horizontal force on upper pad by central differences
dy := .0001
do_yforce := { oldshift := shift; shift := shift + dy;
set vertex y y+dy*z/zh; // uniform shear
recalc;
energy1 := total_energy -
body[1].pressure*(body[1].volume - body[1].target);
oldshift := shift; shift := shift - 2*dy;
set vertex y y-2*dy*z/zh; // uniform shear
recalc;
energy2 := total_energy -
body[1].pressure*(body[1].volume - body[1].target);
yforce := -(energy1-energy2)/2/dy;
printf "restoring force: %20.15f\n",yforce;
// restore everything
oldshift := shift; shift := shift + dy;
set vertex y y+dy*z/zh; // uniform shear
recalc;
}
// vertical force on upper pad by central differences.
dz := .0001
do_zforce := { oldzh := zh; zh := zh + dz;
set vertex z z+dz*z/oldzh; recalc; // uniform stretch
energy1 := total_energy -
body[1].pressure*(body[1].volume - body[1].target);
oldzh := zh; zh := zh - 2*dz;
set vertex z z-2*dz*z/oldzh; recalc; // uniform stretch
energy2 := total_energy -
body[1].pressure*(body[1].volume - body[1].target);
zforce := -(energy1-energy2)/2/dz;
printf "vertical force: %20.15f\n",zforce;
// restore everything
oldzh := zh; zh := zh + dz;
set vertex z z+dz*z/oldzh; recalc; // uniform stretch
}