Back to top of Surface Evolver documentation.
Index.
Hessian, Eigenvalues, Eigenvectors, and Stability
in the Surface Evolver
Our motto: The purpose of calculus is to turn every problem
into a linear algebra problem.
Contents:
- How to think of surfaces discretized in the Evolver.
- What is the Hessian?
- Eigenvalues and eigenvectors.
- Physical interpretation of eigenvalues and eigenvectors.
- Eigenprobe command.
- Ritz command.
- The Square example.
- Hessian with metric.
- Normal motion mode.
- Visualizing eigenvectors.
- Hessian iteration.
- Hessian_seek.
- Saddle.
- Unstable surfaces.
- Accuracy of eigenvalues.
- Caveats and warnings.
For background,
see any decent linear algebra text, such as Strang [SG], especially chapter 6.
For more on stability and bifurcations, see Arnol'd [AV] or Hale and
Kocak [HK].
1. How to think of surfaces discretized in the Evolver.
The Surface Evolver parameterizes a surface in terms of vertex
coordinates. Restrict attention to one fixed triangulation
of a surface. Let X be the vector of all vertex coordinates,
containing N entries, where N could be thousands. Call X the
"configuration vector", and call the N-dimensional vector space
it inhabits "configuration space". The total energy E(X) is
a scalar function on configuration space. Visualize the graph
of the energy function as a rolling landscape with mountains, valleys,
and mountain passes. The gradient of the energy is the steepest
uphill direction. The ordinary
'g' iteration step of Evolver
minimizes energy by moving in the downhill direction, the negative
of the gradient direction, seeking a local minimum.
A constraint is a scalar function on configuration space
such that X is restricted to lie on a particular level set. A
global constraint, such
as a volume constraint, determines a hypersurface, that is, it removes one
degree of freedom from the configuration space.
Level-set constraints
on vertices,
such as x^2 + y^2 = 4, are actually a separate constraint for each vertex
they apply to. Each removes one degree of freedom for each vertex
it applies to. The intersection of all the constraint hypersurfaces
is called the "feasible set", and is the set of all possible
configurations satisfying all the constraints. If there are any nonlinear
constraints, such as curved walls or volume constraints, then the
feasible set will be curved. When a surface is moved, by
'g' for
example, the vector for the direction of motion is always first
projected to be tangent to the feasible set. However, if the
feasible set is curved, straight-line motion will deviate
slightly from the feasible set. Therefore, after every motion
X is projected back to the feasible set using Newton's Method.
2. What is the Hessian?
Consider a particular surface in a particular configuration X,
and consider a small perturbation Y added to X. Then the energy
may be expanded in a Taylor series:
E(X+Y) = E0 + GT Y + 1/2 YT H Y + ...
Here the constant E0 is the original energy, E0 = E(X).
G is the vector of first derivatives, the gradient, which is a
vector the same dimension as Y or X (GT is a 1-form, if you want
to get technical).
Here T denotes the transpose.
H is the square matrix of second
derivatives, the Hessian.
The Hessian
is automatically a symmetric matrix. The gradient G determines the
best linear approximation to the energy, and the Hessian H determines
the best quadratic approximation.
Positive definiteness.
If the quadratic term 1/2 YT H Y is always positive for
any nonzero Y, then H is said to be positive definite.
At an equilibrium point, this means the point is a strict local minimum;
this is the multivariable version of the second derivative test for
a minimum. If the quadratic term is zero or positive, then
H is positive semi-definite. No conclusion can be drawn
about being a local minimum, since third-order terms may prevent that.
If the quadratic term has positive and negative values, then H is
indefinite.
Constraints. If there are constraints on the surface,
then the the perturbation
vector Y is required to be tangent to the feasible set in configuration
space. The curvature of the feasible set can have an effect on H,
but this is taken care of automatically by the Evolver. This effect
arises from the slight change in energy due to the projection back
to the feasible set after motion. This does not affect the gradient,
but it does affect the Hessian. In particular, if Q is the Hessian
of a global constraint and q is the Lagrange multiplier for the constraint,
then the adjusted energy Hessian is H - qQ. Therefore it is necessary
to do a 'g' step to calculate Lagrange
multipliers before doing any Hessians when there are global constraints.
3. Eigenvalues and eigenvectors.
The Hessian H is a real symmetric matrix. Therefore it can
be diagonalized by an orthogonal change of basis of configuration space.
The new basis vectors are called eigenvectors, and the entries
on the diagonal version of H are called eigenvalues.
In this eigenvector
basis, the shape of the graph of the quadratic term becomes obvious.
Directions
along eigenvectors with negative eigenvalues have curvature
downward. Directions with positive eigenvalues have upward
curvature. Remember that eigenvectors are in configuration
space, so each eigenvector represents a particular perturbation
of the surface.
Another characterization of an eigenvector Q with an eigenvalue q
is
H Q = q Q.
which is obvious in an eigenvector basis, but serves to define
eigenvectors in an arbitrary basis.
Index and inertia.
The number of negative eigenvalues of H is called the index of H.
The triple of numbers of negative, zero, and positive eigenvalues is called
the inertia of H. One can also speak of the inertia relative
to a value c as the inertia of H-cI, i.e. the number of eigenvalues
less than c, equal to c, and greater than c.
Sylvester's Law of Inertia says that if P is a nonsingular matrix
of the same dimension as H, then the matrix
K = P H PT
has the same inertia as H, although not the same eigenvalues. The
Evolver can factor a Hessian into a form
H = L D LT
where L is a lower triangular matrix and D is diagonal. Hence the
inertia of H can be found by counting signs on the diagonal of D.
Inertia relative to c can be found by factoring H-cI.
The eigenvectors associated to a particular eigenvalue form a
subspace, whose dimension is called the "multiplicity" of the
eigenvalue.
With volume constraints. If a surface is subject to
volume constraints or named quantity constraints, these are taken
into account in calculating eigenvalues and eigenvectors. In particular,
when defining a perturbation by a vectorfield, projection back to
the constraints is done at the end of the projection. So for a
nonlinear volume constraint (which is usually the case), adding
a volume constraint is different than taking the eigenvalues of
the unconstrained hessian relative to a linear subspace. It can
happen that adding a constraint can have a lower lowest eigenvalue
than without the constraint.
4. Physical interpretation of eigenvalues and eigenvectors.
One can think of an eigenvector as a mode of pertubation of the surface,
and the corresponding eigenvalue an indicator of its stability.
Consider a surface at equilibrium. Recall that the gradient after a
small perturbation from equilibrium is
grad E = H Y.
So if we move along an eigenvector direction,
grad E = H Q = q Q.
Note the force is aligned exactly with the perturbation. Since
force is negative gradient, if q is positive the force will
restore the surface to equilibrium (stable perturbation),
and if q is negative the
force will cause the pertubation to grow (unstable perturbation).
Each eigenvector thus
represents a mode of perturbation. Furthermore, different modes
grow or decay independently, since in an eigenvector basis the
Hessian is diagonal and there are no terms linking the different
modes.
5. Eigenprobe command
The inertia of the Hessian with respect to some value
may be found with the eigenprobe
command.
The syntax to find the inertia relative to a probe value c is
"eigenprobe c".
For example, "eigenprobe 1"
would report the number of eigenvalues less than 1, equal to 1,
and greater than 1. For example, suppose we use cube.fe, and
do "r; r; g 5; eigenprobe 1". Then we get
Vertices: 50 Edges: 144 Facets: 96 Bodies: 1 Facetedges: 288
Element memory: 39880
Total data memory: 294374 bytes.
Enter command: r
Vertices: 194 Edges: 576 Facets: 384 Bodies: 1 Facetedges: 1152
Element memory: 157384
Total data memory: 422022 bytes.
Enter command: g 5
5. area: 5.35288108682446 energy: 5.35288108682446 scale: 0.233721
4. area: 5.14937806689761 energy: 5.14937806689761 scale: 0.212928
3. area: 5.04077073041990 energy: 5.04077073041990 scale: 0.197501
2. area: 4.97600054126748 energy: 4.97600054126748 scale: 0.213378
1. area: 4.93581733363156 energy: 4.93581733363156 scale: 0.198322
Enter command: eigenprobe 1
Eigencounts: 18 <, 0 ==, 175 >
This means the Hessian has 18 eigenvalues less than 1, none equal to 1,
and 175 greater than 1. Note the total number of eigenvalues is equal
to the total number of degrees of freedom of the surface, in this
case
(# vertices)-(# constraints) = 194 - 1 = 193 = 18+175
where the constraint is the volume constraint. Why there is one
degree of freedom per vertex instead of three is explained below in
the normal_motion section.
6. Ritz command
For calculation of eigenvalues near a particular probe value,
there is the ritz
command (named after the Rayleigh-Ritz algorithm). The syntax is
"ritz(c,n)", where c is the probe value and n is the desired
number of eigenvalues.
For example, evolve cube.fe with "g 5; r; g 5; r; g 5",
and do "ritz(0,5)".
You should get output like this:
Enter command: ritz(0,5)
Eigencounts: 0 <, 0 ==, 193 >
1. 0.001687468263013
2. 0.001687468263013
3. 0.001687468263013
4. 0.2517282974725
5. 0.2517282974731
Iterations: 710. Total eigenvalue changes in last iteration: 4.0278891e-013
The first line of output is the inertia, exactly as in eigenprobe. Then
come the eigenvalues as the algorithm finds them, usually in order away
from the probe value.
How ritz works: For ritz(c,n), Evolver creates a random
n-dimensional subspace and applies shifted inverse iteration to it,
i.e. repeatedly applies (H - cI)-1 to the subspace and
orthonormalizes it. Eigenvalues of H near p correspond to large
eigenvalues of (H - cI)-1, so the corresponding eigenvector
components grow by large factors each inverse iteration.
Evolver reports eigenvalues as they converge to machine precision. When all
desired eigenvalues converge (as by the total change in eigenvalues in an
iteration being less than 1e-10), the iteration ends and the values are
printed. Lesser precision is shown on these to indicate they are not
converged to machine precision. You can interrupt ritz by hitting the
interrupt key (usually CTRL-C), and it will report the current eigenvalue
approximations.
NOTE: It is best to use probe values below the
least eigenvalue, so H-cI is positive
definite. Makes the factoring more numerically stable.
7. The Square example
We now explore the eigenvalues of a very simple surface, a flat square
with fixed sides. For a continuous surface, classical calculus of variations
reveals that the Hessian for area is the Laplace operator. For
a square of side length pi, this has eigenvalues m2 + n2
for m,n = 1,2,3,..., or in ascending sequence
2, 5, 5, 8, 10, 10, 13, 13, 17, 17, ..
(you may remember this from PDE analysis of the heat
equation). Run the datafile square.fe and refine it twice (no need to
evolve, since it is already flat). Do "ritz(0,10)".
Enter command: ritz(0,10)
Eigencounts: 0 <, 0 ==, 25 >
1. 0.585786437626905
2. 1.386874070247247
3. 1.386874070247247
4. 2.000000000000000
5. 2.585786437626905
6. 2.585786437626906
7. 2.917607799707606
8. 2.9176077997076
9. 3.4142135623733
10. 4.0000000000000
Doesn't look exactly like we expected. It does have multiplicity two
eigenvalues in the right places, though. Maybe we haven't refined enough.
Refine again and do "ritz(0,10)". You get
Enter command: ritz(0,10)
Eigencounts: 0 <, 0 ==, 113 >
1. 0.152240934977427
2. 0.375490214588449
3. 0.375490214588449
4. 0.585786437626905
5. 0.738027372604331
6. 0.738027372604331
7. 0.927288973154334
8. 0.927288973154335
9. 1.225920309355705
10. 1.2259203093583
Things are getting worse! The eigenvalues all shrunk drastically! They
are not converging! What's going on? The next section explains.
8. Hessian with metric.
One would expect that refining the surface would lead the eigenvalues
to converge to the eigenvalues for the smooth surface. But as the
previous section showed, refining caused the eigenvectors to all
shrink by about a factor of 4. This is no
way to converge. The explanation is that so far we have been
looking at eigenvectors in slightly the wrong way. An eigenvector
is supposed to represent a mode of perturbation that is proportional
to the force. However, the response of a surface to a force need
not be numerically equal to the force. After all, forces and
displacements are different kinds of things. They have different
units: displacement has units of distance, and force has units
of energy per distance. In other words, displacement is a vector
and force is a covector. Note that matrix multiplication by
the Hessian H turns a vector into
a covector. In general, to turn a vector into an equivalent covector, one
needs an inner product, or metric. So far we have been using the Euclidean
inner product on configuration space, but that is not the proper
one to use if you want to approximate smooth surfaces. The
proper inner product of perturbations f and g of a smooth surface
is the integral over the surface of the pointwise inner product:
/
<f,g> = | <f(x),g(x)> dA.
/
In discrete terms, the inner product takes the form of a square
matrix M such that <Y,Z> = YT M Z for vectors Y,Z. We want
this inner product to approximate integration with respect to
area. Having such an M, the eigenvalue equation becomes
H Q = q M Q.
Officially, Q is now called a "generalized eigenvector" and q is a
"generalized eigenvalue". But we will drop the "generalized".
An intuitive interpretation of this equation is as Newton's Law
of Motion,
Force = Mass * Acceleration
where HQ is the force, M is the mass, and qQ is the acceleration.
In other words, in an eigenmode, the acceleration is proportional
to the perturbation.
The Evolver toggle command
"linear_metric"
includes M in the eigenvector
calculations. Two metrics are available. In the simplest,
the "star metric", M is a diagonal matrix, and the "mass" associated with
each vertex is 1/3 of the area of the adjacent facets (1/3 since each
facet gets shared among 3 vertices). The other, the "linear metric",
extends functions from vertices to facets by linear interpolation
and integrates with respect to area. By default, "linear_metric"
uses a 50/50 mix of the two, which seems to work best. See the
more detailed discussion below in the
eigenvalue accuracy section. The fraction of linear metric
can be set by assigning the fraction to the internal variable
linear_metric_mix.
By default, linear_metric_mix is 0.5. In quadratic mode, however,
only the quadratic interpolation metric is used, since the star metric
restricts convergence to order h2 while the quadratic interpolation
metric permits h4 convergence.
Example: Run square.fe, and refine twice. Do "linear_metric" and
"ritz(0,10)".
Enter command: linear_metric
Using linear interpolation metric with Hessian.
Enter command: ritz(0,10)
Eigencounts: 0 <, 0 ==, 25 >
1. 2.036549240354335
2. 4.959720306550875
3. 4.959720306550875
4. 7.764634143334637
5. 10.098798069316683
6. 10.499717069102575
7. 12.274525789880887
8. 12.274525789880890
9. 15.7679634642721
10. 16.7214142904405
Iterations: 127. Total eigenvalue changes in last iteration: 1.9602375e-014
After refining again:
Enter command: ritz(0,10)
Eigencounts: 0 <, 0 ==, 113 >
1. 2.009974216370147
2. 4.999499042685446
3. 4.999499042685451
4. 7.985384943789077
5. 10.090156419079085
6. 10.186524915471155
7. 13.008227978344527
8. 13.008227978344527
9. 17.242998229925817
10. 17.2429982299600
Iterations: 163. Total eigenvalue changes in last iteration: 1.9186042e-014
This looks much more convergent.
Using linear_metric does NOT change the inertia of the Hessian, by
Sylvester's Law of Inertia. So the moral of the story is that if
you care only about stability, you don't need to use linear_metric.
If you do care about the actual values of eigenvectors, and want them
relatively independent of your triangulation, then use linear_metric.
9. Normal motion mode.
The alert reader will have notice that in the examples so far there
has been only one degree of freedom per vertex, instead of the three
one might expect, since a vertex has three degrees of freedom to
move in space. The answer is that in Hessian activities, it is usually
best to only allow motion perpendicular to the surface, and suppress
the two degrees of freedom of motion of a vertex tangential to the
surface. The reason is that tangential motion changes the energy
of the surface very little if at all, leading to many small eigenvalues
and a severely singular Hessian. For example, run square.fe, refine twice,
and do "hessian_normal off" to
enable all degrees of freedom. Now
"eigenprobe 0" reveals 50 zero eigenvalues:
Enter command: hessian_normal off
hessian_normal OFF. (was on)
Enter command: eigenprobe 0
Eigencounts: 0 <, 50 ==, 25 >
For a curved surface, the extra eigenvalues generally won't be zero, but
they will all be close to zero, both positive and negative, which can
really foul things up. The default value of hessian_normal is therefore
the ON state. The moral of the story is to always leave hessian normal
on, unless you really really know what you are doing.
On some surfaces, for example soap films with triple junctions and
tetrahedral points, there are vertices with no natural normal vector.
Evolver hessian_normal mode assigns those points normal subspaces
instead, so that vertices on a triple line can move in a two-dimensional
normal space perpendicular to the triple line, and tetrahedral points
can move in all three dimensions.
The reason for possible negative extra eigenvalues when hessian_normal
is off is that one rarely has the best possible vertex locations
for a given triangulation of
a surface, even when its overall shape is very close to optimal.
Vertices always seem to want to slither sideways to save very very
small amounts of energy. The amount of energy saved this way is
usually much less than the error due to discrete approximation,
so it is usually advisable not to try to get the absolute best
vertex positions.
There is one effect of hessian_normal that may be a little puzzling
at first. Many times a surface is known to have modes with zero
eigenvalue; translational or rotational modes, for example. Yet
no zero eigenvalues are reported. For example, with the cube
eigenvalues found above,
Eigencounts: 0 <, 0 ==, 193 >
1. 0.001687468263013
2. 0.001687468263013
3. 0.001687468263013
4. 0.2517282974725
5. 0.2517282974731
one might expect 6 zero eigenvalues from three translational modes and
three rotational modes. But the rotational modes are eliminated
by the hessian_normal restriction. The three translational modes
have eigenvalue near 0, but not exactly 0, since normal motion can
approximate the translation of a cube, but not exactly.
The effective translation results
from vertices moving in on one hemisphere and out on the other.
This distorts the triangulation, raising the energy, hence the
positive eigenvalue. This effect decreases with refinement.
There are times when the normal direction is not the direction
one wants. If one knows the perturbation direction, one can use
the
hessian_special_normal feature to use that instead of the default
normal. Beware that
hessian_special_normal also applies to the normal calculated by
the vertex_normal
attribute and the normal
used by regular vertex averaging.
10. Visualizing eigenvectors.
Naturally, you want to see what various modes look like. At present.
Evolver can do this through a subsidiary menu invoked by the
command "hessian_menu".
This is a menu I use to test out various Hessian-related features.
| Option | Action |
|
1 | Initialize Hessian. |
|
Z | Do ritz calculation of multiple eigenpairs. This
prompts for a shift value. Pick a value near the
eigenvalues you want, preferably below them so the
shifted Hessian is positive definite. This also
prompts for a number of eigenpairs to do. Eigenvalue
approximations are printed as they converge. You
can stop the iterations with a keyboard interrupt. |
|
X | Pick which eigenvector you want to use for moving.
You can enter
the eigenvector by its number in the list from the Z option.
As a special bonus useful when there are multiple eigenvectors for an
eigenvalue, you can enter the vector as a linear combination of
eigenvectors, e.g. "0.4 v1 + 1.3 v2 - 2.13 v3". |
|
4 | Move. This prompts you for a scale factor. 1 is a
reasonable first guess. If it is too big or too
small, option 7 restores the original surface so
you can try option 4 again. |
|
7 | Restore original surface. Do this unless you want
your surface to stay moved when you exit hessian_menu.
Can repeat cycle by doing option X again. |
|
q | Quit back to main prompt. The surface is not
automatically restored to its original state. Be
sure to do option 7 before quitting if you don't
want to keep the changes! |
Square example. Let us see how to display the lower eigenmodes
for the square, pictured here:


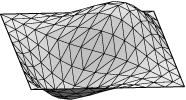

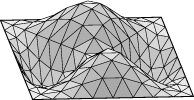
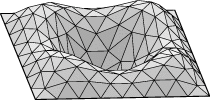

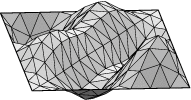
Run square.fe, display, and refine three times. Run "linear_metric".
Run "hessian_menu". At the hessian_menu prompt, do option 1 (which
calculates the Hessian matrix),
then option z (ritz command) and respond to the prompt for number
of eigenvectors with 10, then option x and pick eigenvector 1.
Then pick option 4 and Step size 1. You should see the mode displayed
in the graphics window. Your image may look the opposite of the first
one pictured above, since the eigenvector comes out of a random initial
choice and thus may point in the opposite direction of what I got.
After admiring the mode a while, do option 7 to restore the surface.
Then do option 4 again with Step size -1 to see the opposite mode.
Do option 7 to get back to the orignal. By doing the cycle of options
x, 4, and 7 you should be able to look at all the eigenmodes found
by the ritz command.
The eigenvector components used to move vertices are stored
in the v_velocity vertex vector attribute, so you may access them
after exiting hessian_menu, for example
set vertex __x __x + 0.5*v_velocity
Ragged-looking eigenvectors: If you have a volume constraint
and make a large move to show an eigenvector, you may get a bumpy
shape instead of the smooth shape you were expecting. This is because
the surface is projected to the volume constraint after moving in
the eigenvector direction. The eigenvector itself is smooth, but
the projection back to the target volume uses the volume gradient,
which depends very much on the triangulation and need not be smooth.
To see the eigenvector without volume projection, from a command
prompt you can do
set vertex __x __x + 0.5*v_velocity
Hessian_menu can do sundry other things, mostly for my use in
debugging. Would-be gurus can
consult the hessian_menu
command documentation for a smorgasbord of more things to do with the Hessian.
11. Hessian iteration.
Or how to converge really really fast.
Suppose we assume the quadratic approximation to the surface energy is a
good one. Then we can find an equilibrium point by solving for
motion Y that makes the energy gradient zero. Recalling that G and
H depend only on X, the energy gradient as a function of Y is
grad E = GT + YT H.
So we want GT + YT H = 0, or transposing,
G + H Y = 0.
Solving for Y gives
Y = - H-1 G.
This is actually the Newton-Raphson Method applied to the gradient.
The Evolver's "hessian"
command does this calculation and
motion. It works best when the surface is near an equilibrium
point. It doesn't matter if the equilibrium is a minimum,
a saddle, or a maximum. However, nearness does matter. Remember
we are dealing with thousands of variables, and you don't have
to be very far away from an equilibrium for the equilibrium
to not be within the scope of the quadratic approximation.
When it does work, hessian will converge very quickly,
4 or 5 iterations at most.
Example: Start with the cube datafile cube.fe.
Evolve with "r; g 5; r; g 5;". This gets
very close to an equilibrium. Doing hessian a couple of times
gets to the equilibrium:
Enter command: hessian
1. area: 4.85807791572284 energy: 4.85807791572284
Enter command: hessian
1. area: 4.85807791158432 energy: 4.85807791158432
Enter command: hessian
1. area: 4.85807791158431 energy: 4.85807791158431
So Hessian iteration converged in two steps. Furthermore, this is
a local minimum rather than a saddle point, since Evolver did not
complain about a non-positive definite Hessian.
NOTE: The hessian command will work with indefinite Hessians,
as long as there are no eigenvalues too close to zero.
The warning about non-positive definite is for your information;
it is does not mean hessian has failed.
12. Hessian_seek.
Even when the Hessian is positive definite, a hessian iteration
may blow up since the surface is not near enough to the minimum
for the Hessian approximation to be valid. For this circumstance,
the hessian_seek command does the same calculation as the hessian
command, except it does a line search along the direction of motion
for the minimum energy instead of jumping directly to the supposed
equilibrium. Basically, it does the same thing as the 'g' command in
optimizing mode, except using the hessian solution instead of the
gradient.
Cube example. Run cube.fe, and do "g; r; hessian_seek".
Enter command: g
0. area: 5.13907252918614 energy: 5.13907252918614 scale: 0.185675
Enter command: r
Vertices: 50 Edges: 144 Facets: 96 Bodies: 1 Facetedges: 288
Element memory: 40312
Total data memory: 299082 bytes.
Enter command: hessian_seek
1. area: 4.91067149153091 energy: 4.91067149153091 scale: 0.757800
This is kind of a trivial example, since hessian doesn't blow up here.
But in general, when in doubt that hessian will work, use hessian_seek.
If hessian_seek reports a scale near 1, then it is probably safe to
use hessian to get the last few decimal places of convergence.
Hessian_seek cannot be as accurate as hessian at final convergence,
since hessian_seek uses differences of energies, which are very
small near the minimum.
Hessian_seek is safe to use even when the Hessian is not positive
definite. I have sometimes found it surprisingly effective even
when the surface is nowhere near a minimum.
13. Saddle.
Sometimes your surface may reach a saddle point of energy where gradient
descent becomes very very slow or even useless. Or you may be wanting
to use hessian, but there are pesky negative eigenvalues. The obvious
thing to do is pick a negative eigenvalue and move in the eigenvector
direction. You could do it by hand with hessian_menu, but the
saddle
command packages it all nicely. It finds the most negative eigenvector
and does a line search in that direction for the lowest energy.
To see an example, run catbody.fe with the following evolution:
u
body[1].target := 4
g 5
r
g 5
V
V
r
g 10
eigenprobe 0
saddle
Further evolution after saddle is necessary to find the lowest
energy surface; saddle just gives an initial push.
It is not necessary to run "eigenprobe 0" first;
if saddle finds no
negative eigenvalues, it says so and exits without moving the surface.
Saddle is safe to use even when nowhere near an equilibrium point.
14. Detecting the onset of instability and evolving unstable surfaces.
The Hessian features can be used to detect the onset of instability
as some parameter changes, and even evolve unstable equilibrium surfaces.
Instability detection is done by watching eigenvalues with the
ritz
command. As an example, consider a ring of liquid outside a cylinder, with
the volume increasing until the symmetric ring becomes unstable. This
is set up in the datafile catbody.fe, which is just cat.fe with a body
defined from the facets. Run catbody.fe with this initial evolution:
u
g 5
r
g 5
body[1].target := 2
g 5
r
body[1].target := 3
g 5
hessian
hessian
linear_metric
ritz(0,5)
This gives eigenvalues
Eigencounts: 0 <, 0 ==, 167 >
1. 0.398411128930840
2. 0.398411128930842
3. 1.905446082321839
4. 1.905446082321843
5. 4.4342055632012
Note we are still in a stable, positive definite situation, but the
lowest eigenvalues are near enough to zero that we need to take care
in increasing the volume. Try an increment of 0.1:
body[1].target += 0.1
g 5
hessian
hessian
ritz(0,5)
Eigencounts: 0 <, 0 ==, 167 >
1. 0.287925880010193
2. 0.287925880010195
3. 1.775425717998147
4. 1.775425717998151
5. 4.2705109310529
A little linear interpolation suggests try an increment of 0.3:
body[1].target += 0.3
g 5
hessian
hessian
hessian
ritz(0,5)
Eigencounts: 0 <, 0 ==, 167 >
1. 0.001364051154697
2. 0.0013640511547
3. 1.4344757227809
4. 1.4344757227809
5. 3.8350719808531
So we are now very very close to the critical volume. In view of
the coarse triangulation here, it is probably not worth the trouble
to narrow down the critical volume further, but rather refine
and repeat the process. But for now keep this surface running
for the next paragraph.
Evolving into unstable territory
Typically these are surfaces with just a few unstable modes.
The idea is to get close to the desired equilibrium and use
hessian to reach it.
Regular 'g' gradient descent
iteration should not be used. To change the surface,
i.e. to follow an equilibrium curve through a phase diagram,
make small changes to the control parameter and use a couple of
hessian iterations to reconverge each time. Particular care
is needed near bifurcation points, because of the several
equilibrium curves that meet. When approaching a bifurcation
point, try to jump over it so there is no ambiguity as to
which curve you are following. The approach to a bifurcation point
can be detected by watching eigenvalues. An eigenvalue crosses 0
when a surface introduces new modes of instability.
Example: Catbody.fe, continued. With catbody.fe in the nearly-critical
state found above, increase the body volume by steps of .1 and run
hessian a couple of times each step:
body[1].target += .1
hessian
hessian
hessian
hessian
body[1].target += .1
hessian
hessian
hessian
hessian
body[1].target += .1
hessian
hessian
hessian
hessian
So hessian alone is enough to evolve with, as long as you stay
near enough to the equilibrium.
Other methods for evolving unstable surfaces:
- Using symmetry. If the unstable surface is more symmetric than the
stable surfaces, then enforcing symmetry can remove the unstable modes.
For example, a surface of revolution could be retricted to just
a 90 degree wedge between two perpendicular mirror planes (level-set
constraints), with 90 degree contact angles on the planes.
- Using volume constraints. Recall that in general every constraint
removes one degree of freedom in the configuration space. Hence
a volume constraint has the potential to remove one unstable mode.
For example, unstable catenoids can be made stable by adding a
volume constraint and adjusting the volume until the pressure is 0.
15. Eigenvalue Accuracy.
For the hard-core Evolver guru.
The question here is how well the eigenvalues of the discrete surface
approximate the eigenvalues of the smooth surface. This is significant
when deciding the stability of a surface. I present some comparisons
in cases where an analytic result is possible. All are done in
hessian_normal mode with
linear_metric.
Any general theorem on accuracy is difficult, since any of
these situations may arise:
- The discrete surface exists, but the smooth surface does not.
- The smooth surface exists, but the discrete surface does not.
- The smooth and discrete surfaces exist, but their eigenvalues
are not close due to proximity to a bifurcation point.
- The discrete surface is a good approximation to the smooth
surface, and their eigenvalues are close. In general, linear model
eigenvalues will have error on the order h2, where h is a typical
edge length, and quadratic model eigenvalues will have error h4.
Example: Flat square membrane with fixed sides of length pi.
Smooth eigenvalues: n2 + m2,
or 2,5,5,8,10,10,13,13,17,17,18,...
64 facets:
linear_metric_mix:=0 linear_metric_mix:=.5 linear_metric_mix:=1
1. 1.977340485013809 2.036549240354332 2.098934776481970
2. 4.496631115530167 4.959720306550873 5.522143605551107
3. 4.496631115530168 4.959720306550873 5.522143605551109
4. 6.484555753109618 7.764634143334637 9.618809107463317
5. 8.383838160213188 10.098798069316681 12.451997407229225
6. 8.958685299442784 10.499717069102577 12.677342602918362
7. 9.459695221455723 12.274525789880890 17.295660791788656
8. 9.459695221455725 12.274525789880887 17.295660791788663
9. 11.5556960351898 15.7679635512509 23.585015056138165
10. 12.9691115062193 16.7214142904454 23.5850152363232
256 facets:
linear_metric_mix:=0 linear_metric_mix:=.5 linear_metric_mix:=1
1. 1.994813709598124 2.009974216370146 2.025331529636075
2. 4.869774462491779 4.999499042685448 5.135641457408189
3. 4.869774462491777 4.999499042685451 5.135641457408191
4. 7.597129628414264 7.985384943789075 8.411811839672165
5. 9.571559289947587 10.090156419079083 10.639318311067063
6. 9.759745949169531 10.186524915471141 10.665025703718413
7. 12.026114091326091 13.008227978344539 14.149533399632906
8. 12.026114091326104 13.008227978344539 14.149533399632912
9. 15.899097189772919 17.242998229925817 18.8011199268796
10. 15.8990975402264 17.2429983900303 18.8011200311777
1024 facets:
linear_metric_mix:=0 linear_metric_mix:=.5 linear_metric_mix:=1
1. 1.998755557957786 2.002568891165917 2.006394465437547
2. 4.967163232244397 5.0005039961225 5.0342462883517
3. 4.967163232244401 5.0005039961225 5.0342462883517
4. 7.897718646133286 7.9990889953386 8.1028624365882
5. 9.891301374223204 10.0268080202750 10.1637119963890
6. 9.941758861492074 10.0519390576227 10.1658353297015
7. 12.750608847206168 13.0141591049184 13.2878054981609
8. 12.750608847206173 13.0141591049184 13.2878054981609
9. 16.718575011911319 17.0839068189583 17.4625185925160
10. 16.7185751321348 17.0839069326949 17.4625186893608
A curious fact here is that eigenvalues 5 and 6 are identical in
the smooth limit, but are split in the discrete approximation.
This is due to the fact that the 2-dimension eigenspace of the
eigenvalue 10 can have a basis of two perturbations that each
have the symmetry of the square, but are differently affected by
the discretization.
Example: Sphere of radius 1 with fixed volume.
Analytic eigenvalues: (n+2)(n-1), n=1,2,3,...
with multiplicities: 0,0,0,4,4,4,4,4,10,10,10,10,10,10,10
Linear mode, linear_metric_mix:=.5.
24 facets 96 facets 384 facets 1536 facets
1. 0.3064952760319 0.1013854786956 0.0288140848394 0.0078006105505
2. 0.3064952760319 0.1013854786956 0.0288140848394 0.0078006105505
3. 0.3064952760319 0.1013854786956 0.0288140848394 0.0078006105505
4. 2.7132437122162 3.9199431944791 4.0054074145696 4.0036000699357
5. 2.7132437122162 3.9199431944791 4.0054074145696 4.0036000699357
6. 2.7132437122162 3.9199431944791 4.0054074145696 4.0036000699357
7. 3.6863290283837 4.3377418342267 4.1193008989205 4.0347069118257
8. 4.7902142880145 4.3377418342267 4.1193008989205 4.0347069118257
9. 4.7902142880145 9.0031399793203 9.9026247196089 9.9870390309740
10. 6.7380098215325 9.7223042306475 10.0981057119891 10.0387404054572
11. 6.7380098215325 9.7223042306545 10.0981057120367 10.0387404054607
12. 6.7380098215325 9.7223042307334 10.0981057121432 10.0387404055516
13. 8.6898276285107 9.9763109502799 10.1298354477703 10.0466252566958
In quadratic mode (net 4 times as many vertices per facet)
24 facets 96 facets 384 facets 1536 facets
1. 0.0311952242811 0.0025690857791 0.0002802874477 0.0000358409262
2. 0.0311952242812 0.0025690857791 0.0002802874477 0.0000358409262
3. 0.0311952242812 0.0025690857791 0.0002802874477 0.0000358409262
4. 4.2142037235384 4.0160946848738 4.0009978658738 4.0000515986034
5. 4.2142037235384 4.0160946848738 4.0009978658738 4.0000515986034
6. 4.2564592100813 4.0222815310390 4.0014892600742 4.0000883321792
7. 4.2564592100813 4.0222815310390 4.0014892600742 4.0000883321792
8. 4.2564592100813 4.0222815310390 4.0014892600742 4.0000883321792
9. 9.9900660130172 10.1007993043211 10.0076507048408 10.0004402861468
10. 9.9900660130172 10.1007993043271 10.0076507049338 10.0004402861545
11. 9.9900660130173 10.1007993047758 10.0076507050506 10.0004402861829
12. 12.1019587923328 10.1262981041797 10.0089922470136 10.0005516796159
13. 12.1019587923350 10.1262981042009 10.0089922470510 10.0005516796196
14. 12.1019587927495 10.1262981044110 10.0089922470904 10.0005516797052
15. 12.6934178610912 10.1478397915001 10.0106695599620 10.0007050467653
16. Caveats and warnings.
When not near enough to an equilibrium, incautious use of
hessian
can wreck a surface. If you don't know what's going to happen,
save the surface first. Or use hessian_seek.
Or use
hessian_menu, where you can restore
the surface with option 7. Or set
check_increase, which will
abort a hessian iteration that would increase energy. But remember
sometimes hessian should increase energy, for example to satisfy
a volume constraint or reach an unstable equilibrium.
Not all energies have built-in Hessians. If Evolver complains about
lacking a Hessian for a particular energy, you will either have
to forego hessian or find a way to phrase your problem in terms
of an energy with a Hessian.
There are three methods of sparse matrix factoring built into Evolver:
YSMP (Yale Sparse Matrix Package), my own minimal degree algorithm, and
METIS recursive bisection.
The ysmp and
metis_factor toggles can be used to control which is active.
Metis is the best overall, particularly on large surfaces, but requires
a separate download and compilation of the METIS library (but it's easy;
see the installation instructions).
back to Hessian top
Back to top of Surface Evolver documentation.
Index.










