Beating Kelvin's Partition of Space
In 1887, Lord Kelvin asked how to partition space into cells of
volume 1 such that the total area of the interfaces between the
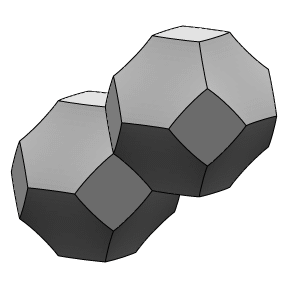
cells is a minimum. The best partition Kelvin could come up with
was made of slightly curved 14-sided polyhedra. Two of Kelvin's
tetrakaidecahedra are pictured here:
For over a century, nobody could improve on Kelvin's partition.
Then in 1993, Denis Weaire and Robert Phelan came up with a partition
of space into two kinds of cells (of equal volume, of course) that
beat Kelvin's partition by 0.3% in area. Ironically, an image with the
same topological structure was in Linus Pauling's 1960
chemistry book
sitting on my father's bookshelf while I tried to beat Kelvin
sitting 10 feet away.
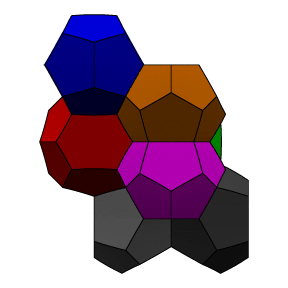
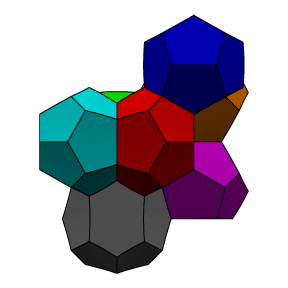
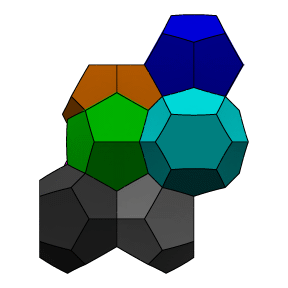
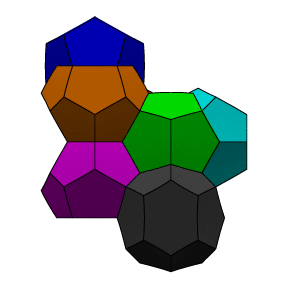
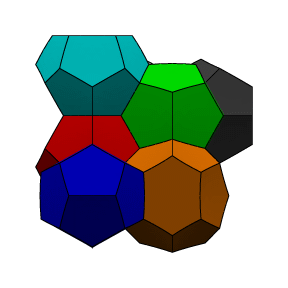
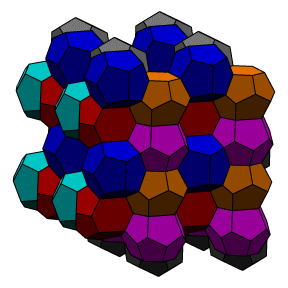
Several views of the
Weaire-Phelan partition are shown below. A fundamental region of
8 different colored cells is shown. Two cells (green and blue)
are dodecahedra, and the other six are 14-sided with two opposite
hexagonal faces and 12 pentagonal faces. The 14-sided cells stack
into three sets of orthogonal columns, and the dodecahedra fit
into the interstices between the columns.
There is no proof that the Weiare-Phelan partition is optimal, or
that Kelvin's partition is optimal for a single shape of cell.
R. Kusner and J. Sullivan have
proved
analytically that the polyhedral
Weaire-Phelan foam beats any foam with the Kelvin topology, removing
any possible doubts about numerical inaccuracies.
The area calculations and these images were made with the
Surface Evolver
program, with the datafiles
twointor.fe for Kelvin's partition, and
phelanc.fe for the Weaire-Phelan partition.
Paper models for building Weaire-Phelan clusters are available from
Stardust.
References:
W. Thomson, Lord Kelvin, "On the division of space with minimum
partitional area", Phil. Mag. vol. 24 (1887), 503.
D. Weaire and R. Phelan, "A counterexample to Kelvin's conjecture
on minimal surfaces", Phil. Mag. Lett. vol. 69 (1994), 107-110.
R. Kusner and J. Sullivan, "Comparing the Weaire-Phelan equal-volume
foam to Kelvin's foam," Forma 11:3, 1996, pp 233-242.
All of the above and others are reprinted in:
D. Weaire et al., The Kelvin Problem, Taylor & Francis, 1996.
Back to
Ken Brakke's home page.