The purpose of Polycut is to illustrate the author's contention that soap films are best viewed as minimal cuts in covering spaces. In particular, any covering space has associated to it a set that is the minimal area cut that can separate the red sheet from the others. To illustrate that, each of the example covering spaces comes with a soap film that may be inserted into the covering space, showing how it blocks all lines of sight to the other sheets. For more about soap films, read section 5 below.
polycutWIN.zip A zip archive containing a Windows 32-bit executable and soap film files.
polycutsrc.tar A source code package for other unix systems with Open GL and for those who wish to modify polycut to include their own spaces.
To install, make a polycut directory and unpack the polycut archive in it. The general unix version will have to have "make" run (good luck!). There is no fancy installation program; all files remain in the polycut directory. When running, the soap film files (extension .off) must be in the current directory or in the directory specified by the environment variable POLYCUTPATH, or else you will not be able to show the soap films.
polycut
Or double-click on the program name, or do whatever you do to launch programs. There are no command line options. All command input to Polycut is through the mouse. Only error messages will appear in the terminal window.
When started, Polycut brings up a graphics window. You must use the mouse to place and size the window as you wish. There is no harm in making it full screen, as there is no other output to look at. The initial view is of a two-sheeted covering space with a circular branch cut.
Mouse commands:
Left button: Rotates the branch curve. Hold the left button down and drag the mouse. The branch curve will rotate as if the mouse is moving a trackball. If you are still moving when you release the left button, the branch curve will continue to rotate. If zoom mode is in effect (see below), then dragging vertically with the left button down will zoom in and out. This is just scaling, not true 3D flight.
Middle button: Rotates the branch curve about the Z axis, that is, clockwise or counterclockwise. Hold down the middle button and drag.
Right button: Brings up the main menu.
Main menu: All the main menu choices have single-key shortcuts, except the new space submenu. Keys are shown in parentheses. You do not need to hit Enter after the key.
New space: Brings up the submenu for choosing covering spaces. If there is no film file for your chosen space, Polycut will print an error message, but everything will still work except displaying the film.
Soap film (f): Toggles showing the soap film corresponding to the current space.
Wire (w): Toggles displaying invisible wires (branch curves of order 1). These display as blue and white dashed curves.
Stop (s): Stops any continuing motion.
Colors (c): Toggles displaying different colored sheets. If OFF, then all background is the color of the viewer's sheet, as if the sheets hadn't been cut and glued together. The branch curve is still shown.
Home sheet (1,2,3,...): Changes the sheet holding the viewpoint.
Rotate (r): Puts left mouse button into rotate mode.
Zoom (z): Puts left mouse button into zoom mode.
Elevation (e): Toggles a window showing top, side, and front view of the branch curve, along with the camera position with respect to each. The camera icon is shown as a T shape. Any of the camera icons can be dragged with the left mouse button to fly around the branch curve. This is the best way to fly through the branch curve to other universes.
Help (h): Prints a help screen to the terminal window.
Quit (q): Exit Polycut.
Mathematically, covering spaces are constructed as follows. Start with a plane (for 2D covering spaces) or Euclidean 3-space (for 3D covering spaces). This is called the "base space". With magic scissors, make cuts in the base space (cuts are lines in the plane or surfaces in 3-space). Make as many copies of this cut base space as you want sheets in your covering space. Then glue each side of a cut on one sheet to the opposite side of the cut on some other sheet (actually, it could be the same sheet). Now everything is smooth, except at the ends of the cuts. These ends are branch points (in 2D) or branch curves (in 3D). If you go around a branch point or curve, you will generally have to make several complete turns to come back to your starting point. The number of turns is called the "order" of the branch point or curve. A branch point or curve of order 1 is just an ordinary point or curve; there is nothing to distinguish it. After the gluing, the cuts become undistinguishable also, so that afterwards there is no way to tell exactly where they were. So in essence, the covering space exists in such a way that the branch points and curves are real but the cuts are artificial.
Another example of a covering space is seen in animated cartoons. A horse disappears behind a skinny tree and doesn't come out the other side. The tree is actually a branch curve, and the horse has gone to another sheet.
The advantage of this model of soap films is that the film becomes an orientable surface, the boundary of the viewer's sheet. This is despite the film being nonorientable in the ordinary sense (mobius band) or having triple junctions or tetrahedral points. Further, there is minimal-cut maximal-flow duality available. Consider the problem of a fluid flowing from the viewer's sheet to the other sheets with the restriction that the the vector difference in flow between any two sheets at corresponding points has maximum magnitude 1. The goal is to maximize the total flux from the viewer's sheet to the other sheets. Then the bottleneck to the flow is precisely the minimal area cut separating the viewer's sheet from the others. Thus we can prove a soap film is indeed the minimal cut by exhibiting a flow whose flux is equal to the area of the film. This is the first technique of proving minimality that is applicable to all soap films. A heavy-duty mathematical treatment of this is available in my preprint "Soap films and covering spaces." (But it has lots of pictures.)
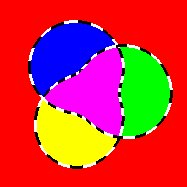
Circle 2-cover. Two sheets with branch curve a circle. Looks the same from front and back since both views see second sheet.
Circle 3-cover. Three sheets with branch curve a circle. Front view sees second sheet, while back view sees third sheet. Covering spaces whose branch curve is an unknotted loop differ only in the number of sheets, i.e. the order of the branch curve. More sheets don't give a different-looking view, since you always see one sheet from the front and another from the back.
Mobius band 2-cover. Two sheets whose branch curve is the edge of a Mobius band. Note that this curve is an unknotted loop, so its covering spaces are topologically the same as those of the circle. But the picture is different since the curve is twisted. Note that the view through the center shows the viewer's home sheet, since in effect the line of sight is going through two cut surfaces, and so gets back to the home sheet. The soap film is a Mobius band. There is no need to have film in the center since going through the center does not lead to another sheet.
Mobius band 3-cover. Three sheets whose branch curve is the edge of a Mobius band. Now going through the center does lead to another sheet, so the soap film extends across the middle. Note that this film has a triple junction line. Triple lines can only appear when the covering space has at least three sheets.
Mobius band 4-cover. One can see four different colors from various angles, but the soap film is the same as the 3-cover. More sheets still give the same film. However, using the method described below for the trefoil 4-cover, one can get the orientable minimal manifold bounded by the wire. It is extremely difficult to get this film physically on a wire, since it would like to make the film shown with the Mobius 3-cover.
Catenoid 2-cover. The branch curves are a pair of coaxial parallel rings. Note the similarity to the Mobius 2-cover. The soap film is a piece of catenoid.
Catenoid 3-cover,symmetric. The gluings around each branch curve are independent. Here the gluings around both rings are the same, so that when you look through the center your line of sight goes through two cuts, from sheet 1 to 2 and then from 2 to 3, and you see a different color background. Hence the soap film must have a disk across the center to block this.
Catenoid 3-cover, antisymmetric. Here the gluings around the two rings are in opposite order, so that looking through the center goes from sheet 1 to 2, then from 2 to 1. Hence the soap film doesn't need to span the center, and winds up being a catenoid again.
Catenoid 4-cover. Both rings branching order 4, parallel gluings.
Double catenoid. The branch curve is two pairs of parallel rings joined at right angles. The curve is topologically an unknotted circle, so covering spaces are distinguished only by the order of branching. This example is an order 3 branching. Note that looking through the centers of the rings always winds up on the viewer's sheet. In fact, there is a continuous path for your line of sight from the middle of a pair of rings between the other pair of rings to the outside. So no covering space of any number of sheets ever gives a different color in the centers. Thus no film has to cover the centers. The film for any order is a double catenoid. Note that this film is not simply connected, even though its boundary is an unknotted closed curve.
Double catenoid with 1 extra wire. If you dip the double catenoid wire into soap solution, you will probably not get the double catenoid film. Instead you will probably get a disk or two spanning the catenoids. But the previous example proved that no covering space gives disks. So how do we get a film with disks? The answer is inspired by the invisible wires of the partial trefoil example. We will put in additional branch curves that wind up being order 1 on sheet 1, yet let us see different background sheets through the centers of the rings. This example adds one invisible wire in the shape of a rectangle (hit 'w' to see it). If one takes the film-with-disk to be the cut between the viewer's sheet and the others, note that the rectangle is of order 1 entirely on the viewer's sheet, hence invisible and not affecting the film's shape, but it is a branch curve of order 2 on the unseen sheets. One way to look at this maneuver is that it converts a film that is a stable relative minimum (as a surface subject to small deformations) in the usual covering space to one that is an absolute minimum in the covering space with the added invisible wire.
Double catenoid with 2 extra wire. Here there are two invisible wire rectangles added. There are four total sheets. The double catenoid wire splits into three branch curves of order 2,1,1, and so do each of the invisible rectangles. The views from the different sheets here are really spectacular.
Trefoil 2-cover. The branch curve is a trefoil knot. The soap film is a Mobius band with 3 half-twists.
Trefoil partial. This is a 3-cover with a trefoil knot branch curve. However, the gluing is done in such a way that there are actually two separate branch curves in the covering space: one is of order 2 and one is of order 1 (note the orders total to 3, which is the number of sheets). Each of these is a complete trefoil. By default, only the order 2 branch curve is shown, since order 1 branch curves are "invisible". You may toggle the showing of invisible branch curves as blue-and-white dashed curves with the "Wires" menu command or by hitting the 'w' key. Note that the two branch curves are entirely separate. To verify this, you can follow each all the way around by changing the viewpoint sheet with the 1,2,3 keys. Going back to sheet 1 and turning off the invisible wires, you see that the soap film doesn't have to touch the full trefoil to cut sheet 1 from the others. Physically, you can form this film by bending a wire into a trefoil and dipping it into soap solution not all the way.
Trefoil full. This is a 3-cover where the branch curve is a trefoil knot with branch order 3. The corresponding soap film spans the full knot, and is what you get when you dip a trefoil wire all the way into soap solution.
Trefoil 4-cover. This is a 4-cover where the branch curve is a trefoil with branch order 4. The standard soap film is the same as the full trefoil case previous. However we're going to change the rules here to get a different film. There is a mathematical theorem that any smooth closed curve is the boundary of a smooth orientable minimal manifold, and none of the previous three films satisfy that. The trefoil 2-cover film was nonorientable, and the next two had triple lines, so were not manifolds. To get the orientable manifold, we make the soap film cut rule that one can glue only consecutive sheets across the cut. That is, sheet 1 in front must be glued to sheet 2 in back, sheet 2 to 3, sheet 3 to 4, and sheet 4 to 1. This guarantees the cut surface is orientable, and it eliminates triple lines since there are no cycles of length 3 permitted (which is what triple junctions are when viewed as cuts). Such a manifold is called a Seifert surface for a knot, and this procedure will produce a Seifert surface for any knot. I have not been able to get this film physically on a wire. It is a genus 1 surface, and soap films don't like to form them naturally. They like to form films with connected exteriors.
Trefoil Narnia. This is a six-fold covering with a single order-2 branch curve that triple covers the trefoil. It is named "Narnia" after a video Bill Thurston made featuring this space.
Figure 8 knot 2-cover. A double covering with an order 2 branch curve in the shape of a figure 8 knot.
Figure 8 knot 3-cover. A triple covering with an order 3 branch curve in the shape of a figure 8 knot.
Figure 8 knot 4-full. A 4-covering with an order 4 branch curve in the shape of a figure 8 knot.
Figure 8 knot 4-partial. A 4-covering with an order 3 branch curve and in the shape of a figure 8 knot. Notice the soap film does not touch one loop of the wire.
Figure 8 knot 5-full. A 5-covering with an order 5 branch curve in the shape of a figure 8 knot.
Figure 8 knot 1,4-cover. A 5-covering with an order 4 branch curve and in the shape of a figure 8 knot. Notice the soap film does not touch one loop of the wire.
Figure 8 knot 2,3-a. A 5-covering with an order 2 and an order 3 branch curve and in the shape of a figure 8 knot.
Figure 8 knot 2,3-b. A different 5-covering with an order 2 and an order 3 branch curve and in the shape of a figure 8 knot.
Figure 8 knot 1,5-cover. A 6-covering with an order 5 branch curve and in the shape of a figure 8 knot. Notice the soap film does not touch one loop of the wire.
Figure 8 knot 2,4-cover. A 6-covering with an order 2 and an order 4 branch curve and in the shape of a figure 8 knot.
Figure 8 knot 3,3-cover. A 6-covering with two order 3 branch curves in the shape of a figure 8 knot.
Figure 8 knot 6-full. A 6-covering with an order 6 branch curve in the shape of a figure 8 knot.
Penetrating loops. The branch curves are two circles of equal radii, one slightly poking through the center of the other. There are three sheets, and each circle splits into two branch curves of orders 2 and 1. So part of one circle is an invisible wire on the viewer's sheet. The soap film is a disk in one circle that is poked up by the other circle. This is an example of a "thin obstacle" problem in minimal surface theory.
Tetrahedron. This is a four-fold covering. The soap film is the tetrahedral minimal cone.
Cube. This is a six-fold covering. The soap film has a rounded square in the middle. Six is the minimal number of sheets for this film without invisible wires.
Octahedron. This is an eight-fold covering. The film is entirely composed of plane segments. Eight is the minimal number of sheets for this film without invisible wires.
Oscillating string. In general relativity, a cosmic string with the negative energy density will have more than 360 degrees around it, so our branch curves could be implemented with the right negative energy density (which is very high). For integral multiples of 360 degrees, space is flat outside the string, so there are none of the nasty gravitational effects associated with ordinary black-hole type wormholes. A curved string would not be static, however, but would obey a fairly simple equation of motion, basically acceleration proportional to curvature. The fascinating point is that it is possible to find solutions where an oscillating loop never intersects itself. This example implements a solution I found in a paper by Turok. It is shown connecting two universes, but could connect any number. In reality, the string would be moving near the speed of light, so you would want a big string and precise timing as you zip through in your spaceship.
To design your own covering space, first decide on your branch curves. Each branch curve may be an open or closed curve, which may be knotted or not. If open curves are used, then more than one curve must attach to any endpoint. One covering space may have any number of branch curves. No branch curve may intersect itself or another branch curve, except at endpoints.
The second step of design is to decide on the gluings across the cut surfaces. The cut surfaces are defined in Polycut to be cones from the origin (center of the screen) out to the curves. That is, the cut surface is swept out by a line segment with one end at the origin and the other end moving along the branch curve. A gluing is specified as a permutation of sheets, that is, for each sheet in front of the cut there is specified which sheet is glued to it in back of the cut, and there is a 1-1 correspondence of sheets. Gluings are completely arbitrary, except for a consistency condition: where two cut surfaces intersect (i.e. where branch curves cross when viewed from the origin), the net permutation due to going through both cut surfaces must be the same on either side of their intersection. This guarantees that the cut surface intersection will not cause a color change in the background. This also means that the cut surfaces get divided up into sections bounded by cut surface intersections, and each section has its own gluing. Sheets may be glued to themselves; this means the arc will be an order 1 branch curve on that sheet, which is an "invisible wire".
The third step is to divide up the branch curves into arcs, one arc for each section of cut surface. Each arc needs to have a C function computing its x, y, and z coordinates as a function of a parameter. This function goes in polydata.c, which contains many examples to follow. Usually, one function can serve for many different arcs, each of which have their own parameter range.
The fourth step is to add a structure to the data[] array in polydata.c. Add it before the last structure, which contains just NULL to signal the end of the array. The fields of this structure are:
The fifth step (optional) is to make a soap film for your covering space. A soap film is represented as a collection of triangles and triple line segments. The format of a soap film file is as follows:
Enter command: read "polycut.cmd"
Enter command: polyfilm >>> "filmfile.off"
Caveat: The polyfilm command assumes all vertices and facets are
consecutively numbered, which means you shouldn't do any surgery
on the surface in Evolver. If you do, dump and reload the surface.
Internally, each branch curve is represented by a linked list of alternating edges and vertices. When it is time to draw a new image, the following steps occur:
A. The coordinates of the vertices are rotated into screen
coordinates.
B. The directions of the links are altered so that all edges
are oriented counterclockwise with respect to the origin
(center of the screen).
C. All vertices are examined to find which are minimums in angle
(i.e. will be encountered by the sweep line before their neighbors).
These are sorted in order of angle. This sweep also identifies
those edges that cross the initial sweep line.
D. The edges crossing the initial sweep line are sorted in order
of the radius of their crossing points.
E. Three lists of upcoming events are set up: endpoints of
active edges, crossings of active edges, and minimum points.
All are kept sorted in order of angle (order the sweep line
will encounter them).
F. As the sweep line rotates around, each event is handled as
it is encountered. An endpoint causes the edges after the
endpoint to replace the old edge in the active edge list (unless
the endpoint is a maximum in angle). A crossing causes a new
vertex to be generated and the edge-vertex links to be rearranged
so the four polygons adjacent to the vertex have proper linked
lists. A minimum causes new edges to be inserted in the
active edge list. Whenever a new edge is added to the active
list, it is checked for intersections with its immediate neighbors.
Crossings found are inserted into the crossings list. The other endpoint
of a new edge is inserted into the endpoint event list.
G. Whenever a crossing or a minimum is encountered, the cuts of
the active edges are sorted in depth order and the coloring of
each segment of the radial line is figured from the cut gluings.
Active edges are marked as to the colors of the inner and outer
adjacent polygons. This step also marks invisible edges.
H. After the sweep has been completed, the polygons are drawn.
The background is cleared to the viewer's sheet color. The
edge list is scanned, and when an edge marked with a color is
found, it starts the drawing of a polygon. The drawing just follows
the edge-vertex linked list around until it comes back to the start.
The polygons are drawn far back in the z-buffer.
I. Finally, the edges are drawn in 3D with the z-buffer. The
branch curves are followed, and visible edges are drawn with
black-and-white dashing, and invisible edges (if turned on)
are drawn blue-and-white.
J. If the soap film is turned on, all its facets are drawn by
just going through the facet list from the film file. Smooth
shading is done by computing the average normal at each vertex
of neighboring facets and having the SGI hardware apply Gourard
shading. The hardware also handles all the coordinate rotation
and z-buffering. Triple lines are then drawn in black moved forward
a little so they are visible.